ParaView/Users Guide/VTK Data Model: Difference between revisions
No edit summary |
No edit summary |
||
| Line 7: | Line 7: | ||
== Mesh == | == Mesh == | ||
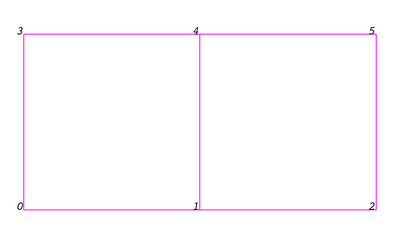
Even though the actual data structure used to store the mesh in memory depends on the type of the dataset, some abstractions are common to all types. We describe these here and we briefly describe the data structures below for each dataset. In general, a mesh consists of vertices (points) and cells (elements, zones). Cells are used to discretize a region and can have various types such a tetrahedra, hexahedra etc. Each cell contains a set of vertices. The mapping from cells to vertices is called the connectivity. Note that even though it is possible to define data elements such as faces and edges, VTK does not represent these explicitly. Rather, they are implied by a cell's type and its connectivity. One exception to this rule is the arbitrary polyhedron which explicitly stores its faces. | Even though the actual data structure used to store the mesh in memory depends on the type of the dataset, some abstractions are common to all types. We describe these here and we briefly describe the data structures below for each dataset. In general, a mesh consists of vertices (points) and cells (elements, zones). Cells are used to discretize a region and can have various types such a tetrahedra, hexahedra etc. Each cell contains a set of vertices. The mapping from cells to vertices is called the connectivity. Note that even though it is possible to define data elements such as faces and edges, VTK does not represent these explicitly. Rather, they are implied by a cell's type and its connectivity. One exception to this rule is the arbitrary polyhedron which explicitly stores its faces. Here is an example mesh that consists of 2 cells. The first cell is defined by vertices (0, 1, 3, 4) and the second cell is defined by vertices (1, 2, 4, 5). These cells are neighbors because they share the edge defined by the points (1, 4). | ||
[[Image:ParaView_UG_Cells.png|400px]] | |||
== Uniform Rectilinear Grid (Image Data) == | == Uniform Rectilinear Grid (Image Data) == | ||
Revision as of 20:26, 10 December 2010
To use ParaView effectively, you need to understand the ParaView data model. Here, we will introduce the the VTK data model used by ParaView briefly. For more details, you can refer to one of the VTK books.
The most fundamental data structure in VTK is a data object. Data objects can either be scientific datasets such rectilinear grids or finite elements meshes (see below) or more abstract data structures such as graphs or trees. Since ParaView is geared toward scientific visualization, we will focus on the former and touch briefly on the latter when necessary.
Datasets are formed of smaller building blocks: mesh (topology and geometry) and attributes.
Mesh
Even though the actual data structure used to store the mesh in memory depends on the type of the dataset, some abstractions are common to all types. We describe these here and we briefly describe the data structures below for each dataset. In general, a mesh consists of vertices (points) and cells (elements, zones). Cells are used to discretize a region and can have various types such a tetrahedra, hexahedra etc. Each cell contains a set of vertices. The mapping from cells to vertices is called the connectivity. Note that even though it is possible to define data elements such as faces and edges, VTK does not represent these explicitly. Rather, they are implied by a cell's type and its connectivity. One exception to this rule is the arbitrary polyhedron which explicitly stores its faces. Here is an example mesh that consists of 2 cells. The first cell is defined by vertices (0, 1, 3, 4) and the second cell is defined by vertices (1, 2, 4, 5). These cells are neighbors because they share the edge defined by the points (1, 4).