#include <vnl_symmetric_eigensystem.h>
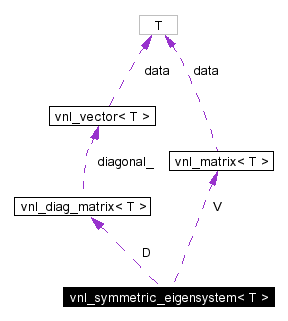
Collaboration diagram for vnl_symmetric_eigensystem< T >:

Public Methods | |
| vnl_symmetric_eigensystem (vnl_matrix< T > const &M) | |
| vnl_vector< T > | get_eigenvector (int i) const |
| T | get_eigenvalue (int i) const |
| vnl_vector< T > | nullvector () const |
| vnl_matrix< T > | recompose () const |
| vnl_matrix< T > | pinverse () const |
| vnl_matrix< T > | square_root () const |
| vnl_matrix< T > | inverse_square_root () const |
| vnl_vector< T > | solve (vnl_vector< T > const &b) |
| void | solve (vnl_vector< T > const &b, vnl_vector< T > *x) |
Public Attributes | |
| vnl_matrix< T > | V |
| vnl_diag_matrix< T > | D |
Protected Attributes | |
| int | n_ |
Definition at line 74 of file vnl_symmetric_eigensystem.h.
|
||||||||||
|
Solve real symmetric eigensystem |
|
||||||||||
|
Recover specified eigenvalue after computation. |
|
||||||||||
|
Recover specified eigenvector after computation. |
|
|||||||||
|
return the inverse of the square root, if positive semi-definite. |
|
|||||||||
|
Convenience method to get least-squares nullvector. It is deliberate that the signature is the same as on vnl_svd<T>. Definition at line 109 of file vnl_symmetric_eigensystem.h. References vnl_matrix< T >::transpose(). |
|
|||||||||
|
return the pseudoinverse. |
|
|||||||||
|
Return the matrix
vnl_symmetric_eigensystem} eig(A);
eig.D.invert_in_place}();
vnl_matrix<double> Ainverse = eig.recompose();
Definition at line 120 of file vnl_symmetric_eigensystem.h. |
|
||||||||||||||||
|
Solve LS problem M x = b. |
|
||||||||||
|
Solve LS problem M x = b. |
|
|||||||||
|
return the square root, if positive semi-definite. |
|
|||||
|
Public eigenvalues.\ After construction, D contains the. eigenvalues, sorted as described above. Note that D is a vnl_diag_matrix, and is therefore stored as a vcl_vector while behaving as a matrix. Definition at line 96 of file vnl_symmetric_eigensystem.h. |
|
|||||
|
Definition at line 83 of file vnl_symmetric_eigensystem.h. |
|
|||||
|
Public eigenvectors.\ After construction, the columns of V are the. eigenvectors, sorted by increasing eigenvalue, from most negative to most positive. Definition at line 90 of file vnl_symmetric_eigensystem.h. |
 1.2.15 written by Dimitri van Heesch,
© 1997-2000
1.2.15 written by Dimitri van Heesch,
© 1997-2000