#include <itkAffineTransform.h>
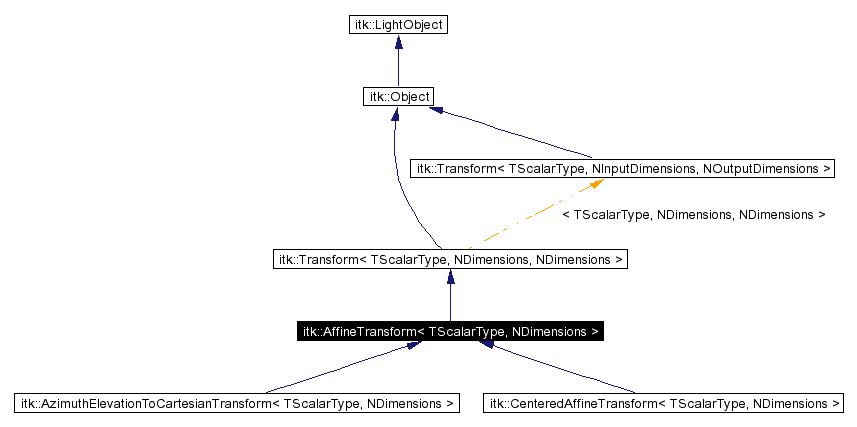
Inheritance diagram for itk::AffineTransform:

Public Types | |
| typedef AffineTransform | Self |
| typedef Transform< TScalarType, NDimensions, NDimensions > | Superclass |
| typedef SmartPointer< Self > | Pointer |
| typedef SmartPointer< const Self > | ConstPointer |
| typedef Superclass::ParametersType | ParametersType |
| typedef Superclass::JacobianType | JacobianType |
| typedef Superclass::ScalarType | ScalarType |
| typedef Matrix< TScalarType, itkGetStaticConstMacro(SpaceDimension), itkGetStaticConstMacro(SpaceDimension) | MatrixType ) |
| typedef OutputVectorType | OffsetType |
| typedef Vector< TScalarType, itkGetStaticConstMacro(SpaceDimension) | InputVectorType ) |
| typedef Vector< TScalarType, itkGetStaticConstMacro(SpaceDimension) | OutputVectorType ) |
| typedef CovariantVector< TScalarType, itkGetStaticConstMacro(SpaceDimension) | InputCovariantVectorType ) |
| typedef CovariantVector< TScalarType, itkGetStaticConstMacro(SpaceDimension) | OutputCovariantVectorType ) |
| typedef vnl_vector_fixed< TScalarType, itkGetStaticConstMacro(SpaceDimension) | InputVnlVectorType ) |
| typedef vnl_vector_fixed< TScalarType, itkGetStaticConstMacro(SpaceDimension) | OutputVnlVectorType ) |
| typedef Point< TScalarType, itkGetStaticConstMacro(SpaceDimension) | InputPointType ) |
| typedef Point< TScalarType, itkGetStaticConstMacro(SpaceDimension) | OutputPointType ) |
Public Methods | |
| virtual const char * | GetClassName () const |
| const OffsetType & | GetOffset (void) const |
| const MatrixType & | GetMatrix () const |
| void | SetOffset (const OffsetType &offset) |
| void | SetMatrix (const MatrixType &matrix) |
| void | SetParameters (const ParametersType ¶meters) |
| const ParametersType & | GetParameters (void) const |
| void | Compose (const Self *other, bool pre=0) |
| void | Translate (const OutputVectorType &offset, bool pre=0) |
| void | Rotate2D (TScalarType angle, bool pre=0) |
| void | Rotate3D (const OutputVectorType &axis, TScalarType angle, bool pre=0) |
| void | Shear (int axis1, int axis2, TScalarType coef, bool pre=0) |
| InputCovariantVectorType | BackTransform (const OutputCovariantVectorType &vector) const |
| InputPointType | BackTransformPoint (const OutputPointType &point) const |
| AffineTransform::Pointer | Inverse (void) const |
| ScalarType | Metric (const Self *other) const |
| ScalarType | Metric (void) const |
| void | PrintSelf (std::ostream &s, Indent indent) const |
| const JacobianType & | GetJacobian (const InputPointType &point) const |
| itkStaticConstMacro (SpaceDimension, unsigned int, NDimensions) | |
| itkStaticConstMacro (ParametersDimension, unsigned int, NDimensions *(NDimensions+1)) | |
| void | SetIdentity (void) |
| const MatrixType & | GetInverse () const |
| void | Scale (const OutputVectorType &factor, bool pre=0) |
| void | Scale (const TScalarType &factor, bool pre=0) |
| void | Rotate (int axis1, int axis2, TScalarType angle, bool pre=0) |
| OutputPointType | TransformPoint (const InputPointType &point) const |
| OutputVectorType | TransformVector (const InputVectorType &vector) const |
| OutputVnlVectorType | TransformVector (const InputVnlVectorType &vector) const |
| OutputCovariantVectorType | TransformCovariantVector (const InputCovariantVectorType &vector) const |
| InputPointType | BackTransform (const OutputPointType &point) const |
| InputVectorType | BackTransform (const OutputVectorType &vector) const |
| InputVnlVectorType | BackTransform (const OutputVnlVectorType &vector) const |
Static Public Methods | |
| Pointer | New () |
Protected Methods | |
| virtual | ~AffineTransform () |
| void | RecomputeInverse () |
| AffineTransform (const MatrixType &matrix, const OutputVectorType &offset) | |
| AffineTransform (unsigned int outputSpaceDimension, unsigned int parametersDimension) | |
| AffineTransform () | |
This class allows the definition and manipulation of affine transformations of an n-dimensional affine space (and its associated vector space) onto itself. One common use is to define and manipulate Euclidean coordinate transformations in two and three dimensions, but other uses are possible as well.
An affine transformation is defined mathematically as a linear transformation plus a constant offset. If A is a constant n x n matrix and b is a constant n-vector, then y = Ax+b defines an affine transformation from the n-vector x to the n-vector y.
The difference between two points is a vector and transforms linearly, using the matrix only. That is, (y1-y2) = A*(x1-x2).
The AffineTransform class determines whether to transform an object as a point or a vector by examining its type. An object of type Point transforms as a point; an object of type Vector transforms as a vector.
One common use of affine transformations is to define coordinate conversions in two- and three-dimensional space. In this application, x is a two- or three-dimensional vector containing the "source" coordinates of a point, y is a vector containing the "target" coordinates, the matrix A defines the scaling and rotation of the coordinate systems from the source to the target, and b defines the translation of the origin from the source to the target. More generally, A can also define anisotropic scaling and shearing transformations. Any good textbook on computer graphics will discuss coordinate transformations in more detail. Several of the methods in this class are designed for this purpose and use the language appropriate to coordinate conversions.
Any two affine transformations may be composed and the result is another affine transformation. However, the order is important. Given two affine transformations T1 and T2, we will say that "precomposing T1 with T2" yields the transformation which applies T1 to the source, and then applies T2 to that result to obtain the target. Conversely, we will say that "postcomposing T1 with T2" yields the transformation which applies T2 to the source, and then applies T1 to that result to obtain the target. (Whether T1 or T2 comes first lexicographically depends on whether you choose to write mappings from right-to-left or vice versa; we avoid the whole problem by referring to the order of application rather than the textual order.)
There are two template parameters for this class:
ScalarT The type to be used for scalar numeric values. Either float or double.
NDimensions The number of dimensions of the vector space.
This class provides several methods for setting the matrix and vector defining the transform. To support the registration framework, the transform parameters can also be set as an Array<double> of size (NDimension + 1) * NDimension using method SetParameters(). The first (NDimension x NDimension) parameters defines the matrix in column-major order (where the column index) varies the fastest). The last NDimension parameters defines the translation or offest in each dimensions.
Add methods to transform (or back transform) many points or vectors at once?
Add reflection? *
Definition at line 112 of file itkAffineTransform.h.
|
|||||
|
Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >, and itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 121 of file itkAffineTransform.h. |
|
|||||
|
Standard covariant vector type for this class Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 154 of file itkAffineTransform.h. |
|
|||||
|
Standard coordinate point type for this class Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >, and itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 168 of file itkAffineTransform.h. |
|
|||||
|
Standard vector type for this class Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 147 of file itkAffineTransform.h. |
|
|||||
|
Standard vnl_vector type for this class Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 161 of file itkAffineTransform.h. |
|
|||||
|
Jacobian Type Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >, and itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 140 of file itkAffineTransform.h. |
|
|||||
|
Standard matrix type for this class Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >, and itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 175 of file itkAffineTransform.h. |
|
|||||
|
Standard offset type for this class Reimplemented in itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 178 of file itkAffineTransform.h. |
|
|||||
|
Standard covariant vector type for this class Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 156 of file itkAffineTransform.h. |
|
|||||
|
Standard coordinate point type for this class Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >, and itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 170 of file itkAffineTransform.h. |
|
|||||
|
Standard vector type for this class Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 149 of file itkAffineTransform.h. |
|
|||||
|
Standard vnl_vector type for this class Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 163 of file itkAffineTransform.h. |
|
|||||
|
Parameters Type Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >, and itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 137 of file itkAffineTransform.h. |
|
|||||
|
Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >, and itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 120 of file itkAffineTransform.h. |
|
|||||
|
Standard scalar type for this class Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >, and itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 143 of file itkAffineTransform.h. |
|
|||||
|
Standard typedefs Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >, and itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 118 of file itkAffineTransform.h. |
|
|||||
|
Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >, and itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 119 of file itkAffineTransform.h. |
|
||||||||||||||||
|
Construct an AffineTransform object This method constructs a new AffineTransform object and initializes the matrix and offset parts of the transformation to values specified by the caller. If the arguments are omitted, then the AffineTransform is initialized to an identity transformation in the appropriate number of dimensions. * |
|
||||||||||||||||
|
Construct an AffineTransform object This method constructs a new AffineTransform object and initializes the matrix and offset parts of the transformation to values specified by the caller. If the arguments are omitted, then the AffineTransform is initialized to an identity transformation in the appropriate number of dimensions. * |
|
|||||||||
|
Construct an AffineTransform object This method constructs a new AffineTransform object and initializes the matrix and offset parts of the transformation to values specified by the caller. If the arguments are omitted, then the AffineTransform is initialized to an identity transformation in the appropriate number of dimensions. * |
|
|||||||||
|
Destroy an AffineTransform object * |
|
||||||||||
|
|
|
||||||||||
|
Back transform by an affine transformation This method finds the point or vector that maps to a given point or vector under the affine transformation defined by self. If no such point exists, an exception is thrown. * |
|
||||||||||
|
Back transform by an affine transformation This method finds the point or vector that maps to a given point or vector under the affine transformation defined by self. If no such point exists, an exception is thrown. * |
|
||||||||||
|
Back transform by an affine transformation This method finds the point or vector that maps to a given point or vector under the affine transformation defined by self. If no such point exists, an exception is thrown. * Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >. |
|
||||||||||
|
Back transform a point by an affine transform This method finds the point that maps to a given point under the affine transformation defined by self. If no such point exists, an exception is thrown. The returned value is (a pointer to) a brand new point created with new. Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >. |
|
||||||||||||||||
|
Compose with another AffineTransform This method composes self with another AffineTransform of the same dimension, modifying self to be the composition of self and other. If the argument pre is true, then other is precomposed with self; that is, the resulting transformation consists of first applying other to the source, followed by self. If pre is false or omitted, then other is post-composed with self; that is the resulting transformation consists of first applying self to the source, followed by other. |
|
|||||||||
|
Run-time type information (and related methods). Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >, and itk::CenteredAffineTransform< TScalarType, NDimensions >. |
|
|||||||||
|
Get inverse matrix of an AffineTransform This method returns the value of the inverse matrix of the AffineTransform. It's not clear that this is useful except for debugging the class itself.
Definition at line 211 of file itkAffineTransform.h. |
|
||||||||||
|
Compute the Jacobian of the transformation This method computes the Jacobian matrix of the transformation. given point or vector, returning the transformed point or vector. The rank of the Jacobian will also indicate if the transform is invertible at this point. Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::CenteredAffineTransform< TScalarType, NDimensions >. |
|
|||||||||
|
Get matrix of an AffineTransform This method returns the value of the matrix of the AffineTransform. Definition at line 190 of file itkAffineTransform.h. References itk::Object::Modified(), and itk::AffineTransform< TScalarType, NDimensions >::RecomputeInverse(). |
|
||||||||||
|
Get offset of an AffineTransform This method returns the offset value of the AffineTransform. * Definition at line 183 of file itkAffineTransform.h. |
|
||||||||||
|
Get the Transformation Parameters. Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::CenteredAffineTransform< TScalarType, NDimensions >. |
|
||||||||||
|
Find inverse of an affine transformation This method creates and returns a new AffineTransform object which is the inverse of self. If self is not invertible, an exception is thrown. * Reimplemented in itk::CenteredAffineTransform< TScalarType, NDimensions >. |
|
||||||||||||||||||||
|
Dimension of the domain space. Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >. |
|
||||||||||||||||||||
|
Dimension of the domain space. Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >, and itk::CenteredAffineTransform< TScalarType, NDimensions >. |
|
||||||||||
|
This method computes the distance from self to the identity transformation, using the same metric as the one-argument form of the Metric() method. * |
|
||||||||||
|
Compute distance between two affine transformations This method computes a ``distance'' between two affine transformations. This distance is guaranteed to be a metric, but not any particular metric. (At the moment, the algorithm is to collect all the elements of the matrix and offset into a vector, and compute the euclidean (L2) norm of that vector. Some metric which could be used to estimate the distance between two points transformed by the affine transformation would be more useful, but I don't have time right now to work out the mathematical details.) |
|
|||||||||
|
New macro for creation of through a Smart Pointer Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >, and itk::CenteredAffineTransform< TScalarType, NDimensions >. |
|
||||||||||||||||
|
Print contents of an AffineTransform Reimplemented from itk::Object. Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >, and itk::CenteredAffineTransform< TScalarType, NDimensions >. |
|
|||||||||
|
Recompute inverse of the transformation matrix * Reimplemented in itk::CenteredAffineTransform< TScalarType, NDimensions >. Referenced by itk::AffineTransform< TScalarType, NDimensions >::GetMatrix(), and itk::AffineTransform< TScalarType, NDimensions >::SetOffset(). |
|
||||||||||||||||||||||||
|
Compose affine transformation with an elementary rotation This method composes self with a rotation that affects two specified axes, replacing the current value of self. The rotation angle is in radians. The axis of rotation goes through the origin. The transformation is given by y[axis1] = cos(angle)*x[axis1] + sin(angle)*x[axis2] y[axis2] = -sin(angle)*x[axis1] + cos(angle)*x[axis2]. All coordinates other than axis1 and axis2 are unchanged; a rotation of pi/2 radians will carry +axis1 into +axis2. The rotation is precomposed with self if pre is true, and postcomposed otherwise. |
|
||||||||||||||||
|
Compose 2D affine transformation with a rotation This method composes self, which must be a 2D affine transformation, with a clockwise rotation through a given angle in radians. The center of rotation is the origin. The rotation is precomposed with self if pre is true, and postcomposed otherwise.
|
|
||||||||||||||||||||
|
Compose 3D affine transformation with a rotation This method composes self, which must be a 3D affine transformation, with a clockwise rotation around a specified axis. The rotation angle is in radians; the axis of rotation goes through the origin. The rotation is precomposed with self if pre is true, and postcomposed otherwise.
|
|
||||||||||||||||
|
Compose affine transformation with a scaling This method modifies self to magnify the source by a given factor along each axis. If all factors are the same, or only a single factor is given, then the scaling is isotropic; otherwise it is anisotropic. If an odd number of factors are negative, then the parity of the image changes. If any of the factors is zero, then the transformation becomes a projection and is not invertible. The scaling is precomposed with self if pre is true, and postcomposed otherwise. |
|
||||||||||||||||
|
Compose affine transformation with a scaling This method modifies self to magnify the source by a given factor along each axis. If all factors are the same, or only a single factor is given, then the scaling is isotropic; otherwise it is anisotropic. If an odd number of factors are negative, then the parity of the image changes. If any of the factors is zero, then the transformation becomes a projection and is not invertible. The scaling is precomposed with self if pre is true, and postcomposed otherwise. |
|
||||||||||
|
Set the transformation to an Identity This sets the matrix to identity and the Offset to null. Reimplemented in itk::CenteredAffineTransform< TScalarType, NDimensions >. Definition at line 196 of file itkAffineTransform.h. |
|
||||||||||
|
Set matrix of an AffineTransform This method sets the matrix of an AffineTransform to a value specified by the user. Definition at line 229 of file itkAffineTransform.h. |
|
||||||||||
|
Set offset (origin) of an Affine Transform. This method sets the offset of an AffineTransform to a value specified by the user. The offset is ...? Definition at line 222 of file itkAffineTransform.h. References itk::Object::Modified(), and itk::AffineTransform< TScalarType, NDimensions >::RecomputeInverse(). |
|
||||||||||
|
Set the transformation from a container of parameters. The first (NDimension x NDimension) parameters define the matrix and the last NDimension parameters the translation. Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::CenteredAffineTransform< TScalarType, NDimensions >. |
|
||||||||||||||||||||||||
|
Compose affine transformation with a shear This method composes self with a shear transformation, replacing the original contents of self. The shear is precomposed with self if pre is true, and postcomposed otherwise. The transformation is given by y[axis1] = x[axis1] + coef*x[axis2] y[axis2] = x[axis2]. * |
|
||||||||||
|
Transform by an affine transformation This method applies the affine transform given by self to a given point or vector, returning the transformed point or vector. The TransformPoint method transforms its argument as an affine point, whereas the TransformVector method transforms its argument as a vector. Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. |
|
||||||||||
|
Transform by an affine transformation This method applies the affine transform given by self to a given point or vector, returning the transformed point or vector. The TransformPoint method transforms its argument as an affine point, whereas the TransformVector method transforms its argument as a vector. Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. Reimplemented in itk::AzimuthElevationToCartesianTransform< TScalarType, NDimensions >. |
|
||||||||||
|
Transform by an affine transformation This method applies the affine transform given by self to a given point or vector, returning the transformed point or vector. The TransformPoint method transforms its argument as an affine point, whereas the TransformVector method transforms its argument as a vector. Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. |
|
||||||||||
|
Transform by an affine transformation This method applies the affine transform given by self to a given point or vector, returning the transformed point or vector. The TransformPoint method transforms its argument as an affine point, whereas the TransformVector method transforms its argument as a vector. Reimplemented from itk::Transform< TScalarType, NDimensions, NDimensions >. |
|
||||||||||||||||
|
Compose affine transformation with a translation This method modifies self to include a translation of the origin. The translation is precomposed with self if pre is true, and postcomposed otherwise. |
 1.2.15 written by Dimitri van Heesch,
© 1997-2000
1.2.15 written by Dimitri van Heesch,
© 1997-2000