Main Page
Groups
Namespace List
Class Hierarchy
Alphabetical List
Compound List
File
List
Namespace Members
Compound Members
File Members
Concepts
itk::MultivariateLegendrePolynomial Class Reference
2D and 3D multivariate Legendre Polynomial
More...
#include <itkMultivariateLegendrePolynomial.h>
List of all members.
Detailed Description
2D and 3D multivariate Legendre Polynomial
In 2D,
![\[ f(x_vector, parameter_vector) = sum_i (sum_j (parameter_{ i j } * P_i(x) *P_j(y)) over j from 0 to l - i)) over i from 0 to l \]](form_155.png)
where P_i() denoting a Legendre polynomial of degree i and l it the degree of the polynomial
In 3D,
![\[ f(x_vector, parameter_vecter) = sum_i (sum_j (sum_k (parameter_{i j k} * P_i(x) * P_j(y) * P_k(z)) over k from 0 to l - i - j) over j from 0 to l - i) over i from 0 to l \]](form_156.png)
The size of the parameter vector for 2D is 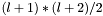 , and for 3D is
, and for 3D is 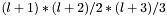
To get the size of the parameter vector, users can use one of the two GetNumberOfCoefficients() member functions
To get function result, users can use the operator() or its SimpleForwardIterator's Get() method.
This is a part of the bias correction methods and implemenations that was initially developed and implemented by Martin Styner, Univ. of North Carolina at Chapel Hill, and his colleagues.
For more details. refer to the following articles. "Parametric estimate of intensity inhomogeneities applied to MRI" Martin Styner, G. Gerig, Christian Brechbuehler, Gabor Szekely, IEEE TRANSACTIONS ON MEDICAL IMAGING; 19(3), pp. 153-165, 2000, (http://www.ia.unc.edu/~styner/docs/tmi00.pdf)
"Evaluation of 2D/3D bias correction with 1+1ES-optimization" Martin Styner, Prof. Dr. G. Gerig (IKT, BIWI, ETH Zuerich), TR-197 (http://www.ia.unc.edu/~styner/docs/StynerTR97.pdf)
Definition at line 70 of file itkMultivariateLegendrePolynomial.h.
Member Typedef Documentation
Constructor & Destructor Documentation
| itk::MultivariateLegendrePolynomial::MultivariateLegendrePolynomial |
( |
unsigned int |
dimension, |
|
|
unsigned int |
degree, |
|
|
const DomainSizeType & |
domainSize |
|
) |
|
|
Member Function Documentation
| void itk::MultivariateLegendrePolynomial::CalculateXCoef |
( |
double |
norm_y, |
|
|
const CoefficientArrayType & |
coef |
|
) |
[protected] |
|
| void itk::MultivariateLegendrePolynomial::CalculateYCoef |
( |
double |
norm_z, |
|
|
const CoefficientArrayType & |
coef |
|
) |
[protected] |
|
| double itk::MultivariateLegendrePolynomial::Evaluate |
( |
IndexType & |
index |
) |
[inline] |
|
|
|
Gets Legendre polynomials' coefficients. |
| unsigned int itk::MultivariateLegendrePolynomial::GetDegree |
( |
void |
|
) |
const [inline] |
|
| unsigned int itk::MultivariateLegendrePolynomial::GetDimension |
( |
void |
|
) |
const [inline] |
|
| const DomainSizeType& itk::MultivariateLegendrePolynomial::GetDomainSize |
( |
void |
|
) |
const [inline] |
|
| unsigned int itk::MultivariateLegendrePolynomial::GetNumberOfCoefficients |
( |
unsigned int |
dimension, |
|
|
unsigned int |
degree |
|
) |
|
|
|
|
Gets the number of coefficients. |
| unsigned int itk::MultivariateLegendrePolynomial::GetNumberOfCoefficients |
( |
|
) |
|
|
|
|
Gets the number of coefficients. |
| unsigned int itk::MultivariateLegendrePolynomial::GetNumberOfCoefficients |
( |
void |
|
) |
const [inline] |
|
| double itk::MultivariateLegendrePolynomial::LegendreSum |
( |
const double |
x, |
|
|
int |
n, |
|
|
const CoefficientArrayType & |
coef, |
|
|
int |
offset = 0 |
|
) |
[protected] |
|
| void itk::MultivariateLegendrePolynomial::Print |
( |
std::ostream & |
os |
) |
|
|
| void itk::MultivariateLegendrePolynomial::PrintSelf |
( |
std::ostream & |
os, |
|
|
Indent |
indent |
|
) |
const [protected] |
|
|
|
Sets the Legendre polynomials' parameters. - Warning:
- The number of coefficients provided should match the number returned by GetNumberOfCoefficients() otherwise an exception is thrown.
|
The documentation for this class was generated from the following file:
Generated at Sat Mar 31 03:02:49 2007 for ITK by  1.3.8 written by Dimitri van Heesch,
© 1997-2000
1.3.8 written by Dimitri van Heesch,
© 1997-2000
![\[ f(x_vector, parameter_vector) = sum_i (sum_j (parameter_{ i j } * P_i(x) *P_j(y)) over j from 0 to l - i)) over i from 0 to l \]](form_155.png)
![\[ f(x_vector, parameter_vector) = sum_i (sum_j (parameter_{ i j } * P_i(x) *P_j(y)) over j from 0 to l - i)) over i from 0 to l \]](form_155.png)
![\[ f(x_vector, parameter_vecter) = sum_i (sum_j (sum_k (parameter_{i j k} * P_i(x) * P_j(y) * P_k(z)) over k from 0 to l - i - j) over j from 0 to l - i) over i from 0 to l \]](form_156.png)
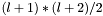 , and for 3D is
, and for 3D is 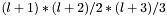
 1.3.8 written by Dimitri van Heesch,
© 1997-2000
1.3.8 written by Dimitri van Heesch,
© 1997-2000