#include <itkMultivariateLegendrePolynomial.h>

Collaboration diagram for itk::MultivariateLegendrePolynomial:

Classes
class	CoefficientVectorSizeMismatch
	Exception object. More...
class	SimpleForwardIterator
	Iterator which only supports forward iteration and Begin(), IsAtEnd(), and Get() method which work just like as SimpleImageRegionIterator. More...
Public Types
typedef DoubleArrayType	CoefficientArrayType
typedef ULongArrayType	DomainSizeType
typedef std::vector< double >	DoubleArrayType
typedef LongArrayType	IndexType
typedef std::vector< long >	LongArrayType
typedef Array< double >	ParametersType
typedef MultivariateLegendrePolynomial	Self
typedef std::vector< unsigned long >	ULongArrayType
Public Member Functions
const CoefficientArrayType &	GetCoefficients (void) const
unsigned int	GetDegree (void) const
unsigned int	GetDimension (void) const
const DomainSizeType &	GetDomainSize (void) const
unsigned int	GetNumberOfCoefficients (void) const
	MultivariateLegendrePolynomial (unsigned int dimension, unsigned int degree, const DomainSizeType &domainSize)
void	SetCoefficients (const CoefficientArrayType &coef) throw ( CoefficientVectorSizeMismatch )
void	SetCoefficients (const ParametersType &coef) throw ( CoefficientVectorSizeMismatch )
virtual	~MultivariateLegendrePolynomial ()
DomainSizeType	m_DomainSize
unsigned int	m_Dimension
unsigned int	m_Degree
unsigned int	m_NumberOfCoefficients
bool	m_MultiplicativeBias
CoefficientArrayType	m_CoefficientArray
CoefficientArrayType	m_CachedXCoef
CoefficientArrayType	m_CachedYCoef
CoefficientArrayType	m_CachedZCoef
DoubleArrayType	m_NormFactor
IndexValueType	m_PrevY
IndexValueType	m_PrevZ
double	Evaluate (IndexType &index)
unsigned int	GetNumberOfCoefficients ()
unsigned int	GetNumberOfCoefficients (unsigned int dimension, unsigned int degree)
void	Print (std::ostream &os)
void	PrintSelf (std::ostream &os, Indent indent) const
double	LegendreSum (const double x, int n, const CoefficientArrayType &coef, int offset=0)
void	CalculateXCoef (double norm_y, const CoefficientArrayType &coef)
void	CalculateYCoef (double norm_z, const CoefficientArrayType &coef)

Detailed Description

2D and 3D multivariate Legendre Polynomial

In 2D,

$f(x_{vector}, parameter_{vector}) = \sum_i^l \left( \sum_j^{l-i} \left( parameter_ {ij} * P_i(x) *P_j(y)) \right) \right)$

where P_i() denoting a Legendre polynomial of degree i and l it the degree of the polynomial

In 3D,

$f(x_{vector}, parameter_{vector}) = \sum_i^l \left( \sum_j^{l-i} \left( \sum_k^{l-i-j} \left( parameter_{ijk} * P_i(x) * P_j(y) * P_k(z) \right) \right) \right)$

The size of the parameter vector for 2D is 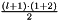$\frac{(l+1)\cdot(1+2)}{2}$ , and for 3D is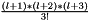 $\frac{(l+1)*(l+2)*(l+3)}{3!}$

To get the size of the parameter vector, users can use one of the two GetNumberOfCoefficients() member functions

To get function result, users can use the operator() or its SimpleForwardIterator's Get() method.

This is a part of the bias correction methods and implemenations that was initially developed and implemented by Martin Styner, Univ. of North Carolina at Chapel Hill, and his colleagues.

Note:: For more details. refer to the following articles. "Parametric estimate of intensity inhomogeneities applied to MRI" Martin Styner, G. Gerig, Christian Brechbuehler, Gabor Szekely, IEEE TRANSACTIONS ON MEDICAL IMAGING; 19(3), pp. 153-165, 2000, (http://www.cs.unc.edu/~styner/docs/tmi99.pdf)

"Evaluation of 2D/3D bias correction with 1+1ES-optimization" Martin Styner, Prof. Dr. G. Gerig (IKT, BIWI, ETH Zuerich), TR-197 (http://www.cs.unc.edu/~styner/docs/StynerTR97.pdf)

Definition at line 74 of file itkMultivariateLegendrePolynomial.h.

Member Typedef Documentation

typedef DoubleArrayType itk::MultivariateLegendrePolynomial::CoefficientArrayType

Internal coefficient storage type.

Definition at line 84 of file itkMultivariateLegendrePolynomial.h.

typedef ULongArrayType itk::MultivariateLegendrePolynomial::DomainSizeType

The size of the domain.

Definition at line 91 of file itkMultivariateLegendrePolynomial.h.

typedef std::vector< double > itk::MultivariateLegendrePolynomial::DoubleArrayType

Definition at line 79 of file itkMultivariateLegendrePolynomial.h.

typedef LongArrayType itk::MultivariateLegendrePolynomial::IndexType

Definition at line 92 of file itkMultivariateLegendrePolynomial.h.

typedef std::vector< long > itk::MultivariateLegendrePolynomial::LongArrayType

Definition at line 81 of file itkMultivariateLegendrePolynomial.h.

typedef Array< double > itk::MultivariateLegendrePolynomial::ParametersType

Same as CoefficientArray This type definition will be used by EnergyFunction object.

Definition at line 88 of file itkMultivariateLegendrePolynomial.h.

typedef MultivariateLegendrePolynomial itk::MultivariateLegendrePolynomial::Self

Definition at line 77 of file itkMultivariateLegendrePolynomial.h.

typedef std::vector< unsigned long > itk::MultivariateLegendrePolynomial::ULongArrayType

Definition at line 80 of file itkMultivariateLegendrePolynomial.h.

Constructor & Destructor Documentation

itk::MultivariateLegendrePolynomial::MultivariateLegendrePolynomial	(	unsigned int	dimension,
		unsigned int	degree,
		const DomainSizeType &	domainSize
	)

Constructor.

virtual itk::MultivariateLegendrePolynomial::~MultivariateLegendrePolynomial ( ) [virtual]

Destructor.

Member Function Documentation

void itk::MultivariateLegendrePolynomial::CalculateXCoef	(	double	norm_y,
		const CoefficientArrayType &	coef
	)		`[protected]`

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

void itk::MultivariateLegendrePolynomial::CalculateYCoef	(	double	norm_z,
		const CoefficientArrayType &	coef
	)		`[protected]`

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

double itk::MultivariateLegendrePolynomial::Evaluate ( IndexType & index ) [inline]

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

Definition at line 155 of file itkMultivariateLegendrePolynomial.h.

const CoefficientArrayType& itk::MultivariateLegendrePolynomial::GetCoefficients ( void ) const

Gets Legendre polynomials' coefficients.

unsigned int itk::MultivariateLegendrePolynomial::GetDegree ( void ) const [inline]

Gets the degree (the degree of Legendre polynomials).

Definition at line 107 of file itkMultivariateLegendrePolynomial.h.

unsigned int itk::MultivariateLegendrePolynomial::GetDimension ( void ) const [inline]

Gets the dimension.

Definition at line 103 of file itkMultivariateLegendrePolynomial.h.

Referenced by itk::MultivariateLegendrePolynomial::SimpleForwardIterator::SimpleForwardIterator().

const DomainSizeType& itk::MultivariateLegendrePolynomial::GetDomainSize ( void ) const [inline]

Gets each dimesion's size.

Definition at line 120 of file itkMultivariateLegendrePolynomial.h.

unsigned int itk::MultivariateLegendrePolynomial::GetNumberOfCoefficients ( void ) const [inline]

Returns the number of coefficients of the polynomial This number is computed from the degree of the polynomial the SetCoefficients() method expects an array of this size, an exception is thrown otherwise

See also:: SetCoefficients

Definition at line 116 of file itkMultivariateLegendrePolynomial.h.

unsigned int itk::MultivariateLegendrePolynomial::GetNumberOfCoefficients ( )

Gets the number of coefficients.

unsigned int itk::MultivariateLegendrePolynomial::GetNumberOfCoefficients	(	unsigned int	dimension,
		unsigned int	degree
	)

Gets the number of coefficients.

double itk::MultivariateLegendrePolynomial::LegendreSum	(	const double	x,
		int	n,
		const CoefficientArrayType &	coef,
		int	offset = `0`
	)		`[protected]`

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

void itk::MultivariateLegendrePolynomial::Print ( std::ostream & os )

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

void itk::MultivariateLegendrePolynomial::PrintSelf	(	std::ostream &	os,
		Indent	indent
	)		const `[protected]`

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

void itk::MultivariateLegendrePolynomial::SetCoefficients ( const CoefficientArrayType & coef ) throw ( CoefficientVectorSizeMismatch )

Sets the Legendre polynomials' parameters.

Warning:: The number of coefficients provided should match the number returned by GetNumberOfCoefficients() otherwise an exception is thrown.

void itk::MultivariateLegendrePolynomial::SetCoefficients ( const ParametersType & coef ) throw ( CoefficientVectorSizeMismatch )

Member Data Documentation

CoefficientArrayType itk::MultivariateLegendrePolynomial::m_CachedXCoef [private]

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

Definition at line 295 of file itkMultivariateLegendrePolynomial.h.

CoefficientArrayType itk::MultivariateLegendrePolynomial::m_CachedYCoef [private]

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

Definition at line 296 of file itkMultivariateLegendrePolynomial.h.

CoefficientArrayType itk::MultivariateLegendrePolynomial::m_CachedZCoef [private]

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

Definition at line 297 of file itkMultivariateLegendrePolynomial.h.

CoefficientArrayType itk::MultivariateLegendrePolynomial::m_CoefficientArray [private]

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

Definition at line 294 of file itkMultivariateLegendrePolynomial.h.

unsigned int itk::MultivariateLegendrePolynomial::m_Degree [private]

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

Definition at line 290 of file itkMultivariateLegendrePolynomial.h.

unsigned int itk::MultivariateLegendrePolynomial::m_Dimension [private]

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

Definition at line 289 of file itkMultivariateLegendrePolynomial.h.

DomainSizeType itk::MultivariateLegendrePolynomial::m_DomainSize [private]

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

Definition at line 288 of file itkMultivariateLegendrePolynomial.h.

bool itk::MultivariateLegendrePolynomial::m_MultiplicativeBias [private]

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

Definition at line 292 of file itkMultivariateLegendrePolynomial.h.

DoubleArrayType itk::MultivariateLegendrePolynomial::m_NormFactor [private]

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

Definition at line 299 of file itkMultivariateLegendrePolynomial.h.

unsigned int itk::MultivariateLegendrePolynomial::m_NumberOfCoefficients [private]

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

Definition at line 291 of file itkMultivariateLegendrePolynomial.h.

IndexValueType itk::MultivariateLegendrePolynomial::m_PrevY [private]

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

Definition at line 300 of file itkMultivariateLegendrePolynomial.h.

IndexValueType itk::MultivariateLegendrePolynomial::m_PrevZ [private]

In the case which the bias field is 2D, it returns bias value at the point which is specified by the index

Definition at line 301 of file itkMultivariateLegendrePolynomial.h.

The documentation for this class was generated from the following file:

itkMultivariateLegendrePolynomial.h

Classes

Public Types

Public Member Functions

Detailed Description

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation