This chapter introduces the basic classes that describe itk::SpatialObjects.
We promote the philosophy that many of the goals of medical image processing are more effectively addressed if we consider them in the broader context of object processing. ITK’s Spatial Object class hierarchy provides a consistent API for querying, manipulating, and interconnecting objects in physical space. Via this API, methods can be coded to be invariant to the data structure used to store the objects being processed. By abstracting the representations of objects to support their representation by data structures other than images, a broad range of medical image analysis research is supported; key examples are described in the following.
In the remainder of this chapter several examples are used to demonstrate the many spatial objects found in ITK and how they can be organized into hierarchies. Further the examples illustrate how to use SpatialObject transformations to control and calculate the position of objects in space.
Spatial objects can be combined to form a hierarchy as a tree. By design, a SpatialObject can have one parent and only one. Moreover, each transform is stored within each object, therefore the hierarchy cannot be described as a Directed Acyclic Graph (DAG) but effectively as a tree. The user is responsible for maintaining the tree structure, no checking is done to ensure a cycle-free tree.
The source code for this section can be found in the file
SpatialObjectHierarchy.cxx.
This example describes how itk::SpatialObject can form a hierarchy. This first example also shows how to create and manipulate spatial objects.
First, we create two spatial objects and give them the names First Object and Second Object, respectively.
We then add the second object to the first one by using the AddChild() method. As a result object2 becomes a child of object1.
Whenever the parameters of an object, including its parent-child relationships are changed, we must then call the Update() method so that the object-to-parent transforms and bounding box internally managed by each object are maintained. Calling Update() on an object automatically causes the Update() function of each child to be called.
object1-¿Update();
To access the list of children of the object, the GetChildren() method returns a pointer to the (STL) list of children.
SpatialObjectType::ChildrenListType ⋆ childrenList = object1->GetChildren();
std::cout << "object1 has " << childrenList->size() << " child" << std::endl;
SpatialObjectType::ChildrenListType::const_iterator it
= childrenList->begin();
while(it != childrenList->end())
{
std::cout << "Name of the child of the object 1: ";
std::cout << (⋆it)->GetProperty().GetName() << std::endl;
++it;
}
Do NOT forget to delete the list of children since the GetChildren() function creates an internal list.
An object can also be removed by using the RemoveChild() method, and then calling Update() on the now-orphaned child.
Then, we can query the number of children an object has with the GetNumberOfChildren() method.
The Clear() method erases all the information regarding the object as well as the data. This method is usually overloaded by derived classes. Note that the Parent-Child relationships of the object are NOT reset when Clear() is called; however, the object-to-parent transform is reset to Identity. As a result, Update() should be called before the object is re-used, to re-compute convenience member variables and values. To remove the children of a node, use the RemoveAllChildren() function.
The output of this first example looks like the following:
The source code for this section can be found in the file
SpatialObjectTransforms.cxx.
s This example describes the different transformations and the Object and World ”spaces” associated with a spatial object.
Several member functions and variables are available to every SpatialObject so that they can readily access the WorldSpace in which they exist:
Like the first example, we create two spatial objects and give them the names First Object and Second Object, respectively.
using SpatialObjectType = itk::SpatialObject<2>;
using TransformType = SpatialObjectType::TransformType;
SpatialObjectType::Pointer object1 = SpatialObjectType ::New();
object1->GetProperty().SetName("First Object");
SpatialObjectType::Pointer object2 = SpatialObjectType ::New();
object2->GetProperty().SetName("Second Object");
object1->AddChild(object2);
First we define a scaling factor of 2 for the object2. This is done by setting the Scale of the ObjectToParentTransform.
Note that this scaling would also apply to the children of object2, if it had children. If you wish to scale an object, but not its children, then those children aren’t actually ”children”, but they are siblings. So, you should insert a that holds the object and its children. Then you can manipulate the object’s transform/scaling independent of its siblings in that group, and if you wish to transform the object and its simblings, you apply that transform to the group.
Next, we apply an offset on the ObjectToParentTransform to object1 which will also cauase a translation of its child, object2.
To realize the previous operations on the transformations, we should invoke the Update() that recomputes all dependent transformations.
By calling this function on object1, it will also descend to its children, thereby also updating the objectToWorldTransform for object2.
We can now display the ObjectToWorldTransform for both objects. One should notice that the only valid members of the Affine transformation are a Matrix and an Offset. For instance, when we invoke the Scale() method the internal Matrix is recomputed to reflect this change.
The AffineTransform performs the following computation
|
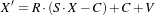| (5.1) |
Where R is the rotation matrix, S is a scaling factor, C is the center of rotation and V is a translation vector or offset. Therefore the affine matrix M and the affine offset T are defined as:
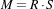 | (5.2) |
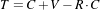 | (5.3) |
This means that Scale() and GetOffset() as well as the GetMatrix() might not be set to the expected value, especially if the transformation results from a composition with another transformation since the composition is done using the Matrix and the Offset of the affine transformation.
Next, we show the two affine transformations corresponding to the two objects.
First, the ObjectToParentTransform for object2:
Second, the ObjectToWorldTransform that is cached, derived from the parent-child hierarchy and the composition of the corresponding ObjectToParentTransform, for object2:
We can also update an object’s ObjectToParentTransform by changing its ObjectToWorldTransform and then calling ComputeObjectToParentTransform(), which changes the ObjectToParentTransform so as to achieve the cached ObjectToWorldTransform.
Finally, we display the resulting affine transformations. First, for the ObjectToParentTransform.
Second, for the ObjectToWorldTransform.
Also, as a child is disconnected from its parent, it should not move; so its ObjectToParentTransform should be updated to match its ]codeObjectToWorldTransform.
object1->RemoveChild( object2 );
object2->Update();
std::cout << "object2 ObjectToWorld Matrix: " << std::endl;
std::cout << object2->GetObjectToWorldTransform()->GetMatrix() << std::endl;
std::cout << "object2 ObjectToWorld Offset: ";
std::cout << object2->GetObjectToWorldTransform()->GetOffset() << std::endl;
std::cout << "object2 ObjectToParent Matrix: " << std::endl;
std::cout << object2->GetObjectToParentTransform()->GetMatrix() << std::endl;
std::cout << "object2 ObjectToParent Offset: ";
std::cout << object2->GetObjectToParentTransform()->GetOffset() << std::endl;
The output of this second example looks like the following:
This section describes in detail the variety of spatial objects implemented in ITK.
The source code for this section can be found in the file
ArrowSpatialObject.cxx.
This example shows how to create an itk::ArrowSpatialObject. Let’s begin by including the appropriate header file.
The itk::ArrowSpatialObject, like many SpatialObjects, is templated over the dimensionality of the object.
The position of the arrow in the object (local) coordinate frame is done using the SetPositionInObjectSpace() method. By default the position is set to the origin of the space. This is the ”tip” of the arrow.
The length of the arrow in the local coordinate frame is done using the SetLengthInObjectSpace() method. By default the length is set to 1. This is the euclidean distance spanned by the arrow’s tail from its tip (position).
The direction of the arrow can be set using the SetDirectionInObjectSpace() method. This is the direction the tail of the arrow extends from the position. By default the direction is set along the X axis (first direction).
The source code for this section can be found in the file
BlobSpatialObject.cxx.
itk::BlobSpatialObject defines an N-dimensional blob. This class derives from itk::itkPointBasedSpatialObject. A blob is defined as a list of points which compose the object.
Let’s start by including the appropriate header file.
BlobSpatialObject is templated over the dimension of the space. A BlobSpatialObject contains a list of SpatialObjectPoints. Basically, a SpatialObjectPoint has a position and a color.
First we declare several standard type definitions.
Every Point-Based SpatialObject also provides type definitions for their SpatialObject point type (e.g., BlobPointType for BlobSpatialObject) as well as for a physical space point (e.g., an itk::Point).
Then, we create a list of points and we set the position of each point in the local coordinate system using the SetPositionInObjectSpace() method. We also set the color of each point to be red.
Next, we create the blob and set its name using the SetName() function. We also set its Identification number with SetId() and we add the list of points previously created and call Update() so that the object can update its transforms, bounding boxes, and other cached convenience member variables.
The GetPoints() method returns a reference to the internal list of points of the object.
Then we can access the points using standard STL iterators and GetPositionInWorldSpace() and GetColor() functions return respectively the position and the color of the point.
GetPositionInWorldSpace applies the objectToParent transforms of all of the parent objects to this point. Since this object has no parents and since this object’s objecttoParent transform is the identify transform (by default), these world space positions are the same as the object space positions that were set.
The source code for this section can be found in the file
EllipseSpatialObject.cxx.
itk::EllipseSpatialObject defines an n-Dimensional ellipse. Like other spatial objects this class derives from itk::SpatialObject. Let’s start by including the appropriate header file.
Like most of the SpatialObjects, the itk::EllipseSpatialObject is templated over the dimension of the space. In this example we create a 3-dimensional ellipse.
Then we set a radius for each dimension. By default the radius is set to 1. Additionally, after setting the SpatialObject’s radius, we call Update() to update all transforms, bounding box, and other convenience variables within the class that its other member functions (e.g., IsInsideInWorldSpace()) depend upon.
Or if we have the same radius in each dimension we can do
We can then display the current radius by using the GetRadiusInObjectSpace() function:
Like other SpatialObjects, we can query the object if a point is inside the object by using the IsInsideInWorldSpace(itk::Point) function. This function expects the point to be in world coordinates.
itk::Point<double,3> insidePoint;
insidePoint.Fill(1.0);
if (myEllipse->IsInsideInWorldSpace(insidePoint))
{
std::cout << "The point " << insidePoint;
std::cout << " is really inside the ellipse" << std::endl;
}
itk::Point<double,3> outsidePoint;
outsidePoint.Fill(3.0);
if (!myEllipse->IsInsideInWorldSpace(outsidePoint))
{
std::cout << "The point " << outsidePoint;
std::cout << " is really outside the ellipse" << std::endl;
}
All spatial objects can be queried for a value at a point. The IsEvaluableAtInWorldSpace() function returns a boolean to know if the object is evaluable at a particular point.
If the object is evaluable at that point, the ValueAtInWorldSpace() function returns the current value at that position. Most of the objects returns a boolean value which is set to true when the point is inside the object and false when it is outside. However, for some objects, it is more interesting to return a value representing, for instance, the distance from the center of the object or the distance from the boundary.
Like other spatial objects, we can also query the bounding box of the object by using GetMyBoundingBoxInWorldSpace(). The resulting bounding box is the world space.
The source code for this section can be found in the file
GaussianSpatialObject.cxx.
This example shows how to create a itk::GaussianSpatialObject which defines a Gaussian in a N-dimensional space. This object is particularly useful to query the value at a point in physical space. Let’s begin by including the appropriate header file.
The itk::GaussianSpatialObject is templated over the dimensionality of the object.
The SetMaximum() function is used to set the maximum value of the Gaussian.
The radius of the Gaussian is defined by the SetRadius() method. By default the radius is set to 1.0.
The standard ValueAt() function is used to determine the value of the Gaussian at a particular point in physical space.
The source code for this section can be found in the file
GroupSpatialObject.cxx.
A itk::GroupSpatialObject does not have any data associated with it. It can be used to group objects or to add transforms to a current object. In this example we show how to use a GroupSpatialObject.
Let’s begin by including the appropriate header file.
The itk::GroupSpatialObject is templated over the dimensionality of the object.
Next, we create an itk::EllipseSpatialObject and add it to the group.
We then translate the group by 10mm in each direction. Therefore the ellipse is translated in physical space at the same time.
We can then query if a point is inside the group using the IsInsideInWorldSpace() function. We need to specify in this case that we want to consider all the hierarchy, therefore we set the depth to 2.
Like any other SpatialObjects we can remove the ellipse from the group using the RemoveChild() method.
The source code for this section can be found in the file
SceneSpatialObject.cxx.
This example describes how to use the itk::GroupSpatialObject. A GroupSpatialObject contains a collection of SpatialObjects. This example begins by including the appropriate header file.
An GroupSpatialObject is templated over the dimension of the space which requires all the objects referenced by the GroupSpatialObject to have the same dimension.
First we define some type definitions and we create the GroupSpatialObject.
Then we create two itk::EllipseSpatialObjects.
Then we add the two ellipses into the GroupSpatialObject.
We can query the number of object in the GroupSpatialObject with the GetNumberOfObjects() function. This function takes two optional arguments: the depth at which we should count the number of objects (default is set to infinity) and the name of the object to count (default is set to ITK_NULLPTR). This allows the user to count, for example, only ellipses.
The GetObjectById() returns the first object in the GroupSpatialObject that has the specified identification number.
Objects can also be removed from the GroupSpatialObject using the RemoveSpatialObject() function.
The list of current objects in the GroupSpatialObject can be retrieved using the GetChildren() method. Like the GetNumberOfChildren() method, GetChildren() can take two arguments: a search depth and a matching name.
In some cases, it is useful to define the hierarchy by using ParentId() and the current identification number. This results in having a flat list of SpatialObjects in the GroupSpatialObject. Therefore, the GroupSpatialObject provides the FixParentChildHierarchyUsingParentIds() method which reorganizes the Parent-Child hierarchy based on identification numbers.
The scene can also be cleared by using the RemoveAllChildren() function.
The source code for this section can be found in the file
ImageSpatialObject.cxx.
An itk::ImageSpatialObject contains an itk::Image but adds the notion of spatial transformations and parent-child hierarchy. Let’s begin the next example by including the appropriate header file.
We first create a simple 2D image of size 10 by 10 pixels.
Next we fill the image with increasing values.
We can now define the ImageSpatialObject which is templated over the dimension and the pixel type of the image.
Then we set the itkImage to the ImageSpatialObject by using the SetImage() function.
At this point we can use IsInside(), ValueAt() and DerivativeAt() functions inherent in SpatialObjects. The IsInside() value can be useful when dealing with registration.
The ValueAtInWorldSpace() returns the value of the closest pixel, i.e no interpolation, to a given physical point.
The derivative at a specified position in space can be computed using the DerivativeAt() function. The first argument is the point in physical coordinates where we are evaluating the derivatives. The second argument is the order of the derivation, and the third argument is the result expressed as a itk::Vector. Derivatives are computed iteratively using finite differences and, like the ValueAt(), no interpolator is used.
The source code for this section can be found in the file
ImageMaskSpatialObject.cxx.
An itk::ImageMaskSpatialObject is similar to the itk::ImageSpatialObject and derived from it. However, the main difference is that the IsInsideInWorldSpace() returns true if the pixel intensity in the image is not zero.
The supported pixel types does not include itk::RGBPixel, itk::RGBAPixel, etc. So far it only allows to manage images of simple types like unsigned short, unsigned int, or itk::Vector. Let’s begin by including the appropriate header file.
The ImageMaskSpatialObject is templated over the dimensionality.
Next we create an itk::Image of size 50x50x50 filled with zeros except a bright square in the middle which defines the mask.
using PixelType = ImageMaskSpatialObject::PixelType;
using ImageType = ImageMaskSpatialObject::ImageType;
using Iterator = itk::ImageRegionIterator< ImageType >;
ImageType::Pointer image = ImageType::New();
ImageType::SizeType size = {{ 50, 50, 50 }};
ImageType::IndexType index = {{ 0, 0, 0 }};
ImageType::RegionType region;
region.SetSize(size);
region.SetIndex(index);
image->SetRegions( region );
image->Allocate(true); // initialize buffer to zero
ImageType::RegionType insideRegion;
ImageType::SizeType insideSize = {{ 30, 30, 30 }};
ImageType::IndexType insideIndex = {{ 10, 10, 10 }};
insideRegion.SetSize( insideSize );
insideRegion.SetIndex( insideIndex );
Iterator it( image, insideRegion );
it.GoToBegin();
while( !it.IsAtEnd() )
{
it.Set( itk::NumericTraits< PixelType >::max() );
++it;
}
Then, we create an ImageMaskSpatialObject.
We then pass the corresponding pointer to the image.
We can then test if a physical itk::Point is inside or outside the mask image. This is particularly useful during the registration process when only a part of the image should be used to compute the metric.
ImageMaskSpatialObject::PointType inside;
inside.Fill(20);
std::cout << "Is my point " << inside << " inside my mask? "
<< maskSO->IsInsideInWorldSpace(inside) << std::endl;
ImageMaskSpatialObject::PointType outside;
outside.Fill(45);
std::cout << "Is my point " << outside << " outside my mask? "
<< !maskSO->IsInsideInWorldSpace(outside) << std::endl;
The source code for this section can be found in the file
LandmarkSpatialObject.cxx.
itk::LandmarkSpatialObject contains a list of itk::SpatialObjectPoints which have a position and a color. Let’s begin this example by including the appropriate header file.
LandmarkSpatialObject is templated over the dimension of the space.
Here we create a 3-dimensional landmark.
Next, we set some properties of the object like its name and its identification number.
We are now ready to add points into the landmark. We first create a list of SpatialObjectPoint and for each point we set the position and the color.
Then we add the list to the object using the SetPoints() method. Calling Update() afterwards ensures that World Space representations are also updated to match changes in the SpatialObject’s parameters.
The current point list can be accessed using the GetPoints() method. The method returns a reference to the (STL) list.
size_t nPoints = landmark->GetPoints().size();
std::cout << "Number of Points in the landmark: " << nPoints << std::endl;
LandmarkType::LandmarkPointListType::const_iterator it
= landmark->GetPoints().begin();
while(it != landmark->GetPoints().end())
{
std::cout << "Position: " << (⋆it).GetPositionInObjectSpace() << std::endl;
std::cout << "Color: " << (⋆it).GetColor() << std::endl;
++it;
}
The source code for this section can be found in the file
LineSpatialObject.cxx.
itk::LineSpatialObject defines a line in an n-dimensional space. A line is defined as a list of points which compose the line, i.e a polyline. We begin the example by including the appropriate header files.
LineSpatialObject is templated over the dimension of the space. A LineSpatialObject contains a list of LineSpatialObjectPoints. A LineSpatialObjectPoint has a position, n-1 normals and a color. Each normal is expressed as a itk::CovariantVector of size N.
First, we define some type definitions and we create our line.
We create a point list and we set the position of each point in the local coordinate system using the SetPosition() method. We also set the color of each point to red.
The two normals are set using the SetNormal() function; the first argument is the normal itself and the second argument is the index of the normal.
LineType::LinePointListType list;
for (unsigned int i=0; i<3; ++i)
{
LinePointType p;
PointType pnt;
pnt[0] = i;
pnt[1] = i+1;
pnt[2] = i+2;
p.SetPositionInObjectSpace(pnt);
p.SetColor(1,0,0,1);
CovariantVectorType normal1;
CovariantVectorType normal2;
for (unsigned int j=0; j<3; ++j)
{
normal1[j]=j;
normal2[j]=j⋆2;
}
p.SetNormalInObjectSpace(normal1,0);
p.SetNormalInObjectSpace(normal2,1);
list.push_back(p);
}
Next, we set the name of the object using SetName(). We also set its identification number with SetId() and we set the list of points previously created.
The GetPoints() method returns a reference to the internal list of points of the object.
Then we can access the points using standard STL iterators. The GetPosition() and GetColor() functions return respectively the position and the color of the point. Using the GetNormal(unsigned int) function we can access each normal.
LineType::LinePointListType::const_iterator it = Line->GetPoints().begin();
while (it != Line->GetPoints().end())
{
std::cout << "Position = " << (⋆it).GetPositionInObjectSpace()
<< std::endl;
std::cout << "Color = " << (⋆it).GetColor() << std::endl;
std::cout << "First normal = " << (⋆it).GetNormalInObjectSpace(0)
<< std::endl;
std::cout << "Second normal = " << (⋆it).GetNormalInObjectSpace(1)
<< std::endl;
std::cout << std::endl;
++it;
}
The source code for this section can be found in the file
MeshSpatialObject.cxx.
A itk::MeshSpatialObject contains a pointer to an itk::Mesh but adds the notion of spatial transformations and parent-child hierarchy. This example shows how to create an itk::MeshSpatialObject, use it to form a binary image, and write the mesh to disk.
Let’s begin by including the appropriate header file.
The MeshSpatialObject wraps an itk::Mesh, therefore we first create a mesh.
using MeshTrait = itk::DefaultDynamicMeshTraits< float, 3, 3 >;
using MeshType = itk::Mesh< float, 3, MeshTrait >;
using CellTraits = MeshType::CellTraits;
using CellInterfaceType = itk::CellInterface< float, CellTraits >;
using TetraCellType = itk::TetrahedronCell< CellInterfaceType >;
using PointType = MeshType::PointType;
using CellType = MeshType::CellType;
using CellAutoPointer = CellType::CellAutoPointer; MeshType::Pointer myMesh = MeshType::New();
MeshType::CoordRepType testPointCoords[4][3]
= { {0,0,0}, {9,0,0}, {9,9,0}, {0,0,9} };
MeshType::PointIdentifier tetraPoints[4] = {0,1,2,4};
int i;
for(i=0; i < 4; ++i)
{
myMesh->SetPoint(i, PointType(testPointCoords[i]));
}
myMesh->SetCellsAllocationMethod(
MeshType::CellsAllocatedDynamicallyCellByCell );
CellAutoPointer testCell1;
testCell1.TakeOwnership( new TetraCellType );
testCell1->SetPointIds(tetraPoints);
We then create a MeshSpatialObject which is templated over the type of mesh previously defined...
... and pass the Mesh pointer to the MeshSpatialObject
The actual pointer to the passed mesh can be retrieved using the GetMesh() function, just like any other SpatialObjects.
The GetBoundingBox(), ValueAt(), IsInside() functions can be used to access important information.
std::cout << "Mesh bounds : "
<< myMeshSpatialObject->GetMyBoundingBoxInWorldSpace()->GetBounds()
<< std::endl;
MeshSpatialObjectType::PointType myPhysicalPoint;
myPhysicalPoint.Fill(1);
std::cout << "Is my physical point inside? : "
<< myMeshSpatialObject->IsInsideInWorldSpace(myPhysicalPoint) << std::endl;
Now that we have defined the MeshSpatialObject, we can save the actual mesh using the itk::SpatialObjectWriter. In order to do so, we need to specify the type of Mesh we are writing.
Then we set the mesh spatial object and the name of the file and call the the Update() function.
Reading the saved mesh is done using the itk::SpatialObjectReader. Once again we need to specify the type of mesh we intend to read.
We set the name of the file we want to read and call update
Next, we show how to create a binary image of a MeshSpatialObject using the itk::SpatialObjectToImageFilter. The resulting image will have ones inside and zeros outside the mesh. First we define and instantiate the SpatialObjectToImageFilter.
Then we pass the output of the reader, i.e the MeshSpatialObject, to the filter.
Finally we trigger the execution of the filter by calling the Update() method. Note that depending on the size of the mesh, the computation time can increase significantly.
Then we can get the resulting binary image using the GetOutput() function.
The source code for this section can be found in the file
SurfaceSpatialObject.cxx.
itk::SurfaceSpatialObject defines a surface in n-dimensional space. A SurfaceSpatialObject is defined by a list of points which lie on the surface. Each point has a position and a unique normal. The example begins by including the appropriate header file.
SurfaceSpatialObject is templated over the dimension of the space. A SurfaceSpatialObject contains a list of SurfaceSpatialObjectPoints. A SurfaceSpatialObjectPoint has a position, a normal and a color.
First we define some type definitions
We create a point list and we set the position of each point in the local coordinate system using the SetPosition() method. We also set the color of each point to red.
SurfaceType::SurfacePointListType list;
for( unsigned int i=0; i<3; i++)
{
SurfacePointType p;
PointType pnt;
pnt[0] = i;
pnt[1] = i+1;
pnt[2] = i+2;
p.SetPositionInObjectSpace(pnt);
p.SetColor(1,0,0,1);
CovariantVectorType normal;
for(unsigned int j=0;j<3;j++)
{
normal[j]=j;
}
p.SetNormalInObjectSpace(normal);
list.push_back(p);
}
Next, we create the surface and set his name using SetName(). We also set its Identification number with SetId() and we add the list of points previously created.
The GetPoints() method returns a reference to the internal list of points of the object.
Then we can access the points using standard STL iterators. GetPosition() and GetColor() functions return respectively the position and the color of the point. GetNormal() returns the normal as a itk::CovariantVector.
SurfaceType::SurfacePointListType::const_iterator it
= surface->GetPoints().begin();
while(it != surface->GetPoints().end())
{
std::cout << "Position = " << (⋆it).GetPositionInObjectSpace()
<< std::endl;
std::cout << "Normal = " << (⋆it).GetNormalInObjectSpace() << std::endl;
std::cout << "Color = " << (⋆it).GetColor() << std::endl;
std::cout << std::endl;
it++;
}
itk::TubeSpatialObject is a class for the representation of tubular structures using SpatialObjects. In particular, it is intended to be used to represent vascular networks extracted from 2D and 3D images. It can also be used to represent airways, nerves, bile ducts, and more.
The class itk::DTITubeSpatialObject is derived from this class and adds constructs for representing fiber tracts from diffusion tensor images.
The source code for this section can be found in the file
TubeSpatialObject.cxx.
itk::TubeSpatialObject defines an n-dimensional tube. A tube is defined as a list of centerline points which have a position, a radius, some normals and other properties. Let’s start by including the appropriate header file.
TubeSpatialObject is templated over the dimension of the space. A TubeSpatialObject contains a list of TubeSpatialObjectPoints.
First we define some type definitions and we create the tube.
We create a point list and we set:
TubeType::TubePointListType list;
for (i=0; i<5; ++i)
{
TubePointType p;
PointType pnt;
pnt[0] = i;
pnt[1] = i+1;
pnt[2] = i+2;
p.SetPositionInObjectSpace(pnt);
p.SetRadiusInObjectSpace(1);
CovariantVectorType normal1;
CovariantVectorType normal2;
for (unsigned int j=0; j<3; ++j)
{
normal1[j]=j;
normal2[j]=j⋆2;
}
p.SetNormal1InObjectSpace(normal1);
p.SetNormal2InObjectSpace(normal2);
p.SetColor(1,0,0,1);
list.push_back(p);
}
Next, we create the tube and set its name using SetName(). We also set its identification number with SetId() and, at the end, we add the list of points previously created.
The GetPoints() method return a reference to the internal list of points of the object.
The ComputeTangentAndNormals() function computes the normals and the tangent for each point using finite differences.
Then we can access the points using STL iterators. GetPosition() and GetColor() functions return respectively the position and the color of the point. GetRadius() returns the radius at that point. GetNormal1() and GetNormal1() functions return a itk::CovariantVector and GetTangent() returns a itk::Vector.
TubeType::TubePointListType::const_iterator it = tube->GetPoints().begin();
i=0;
while(it != tube->GetPoints().end())
{
std::cout << std::endl;
std::cout << "Point #" << i << std::endl;
std::cout << "Position: " << (⋆it).GetPositionInObjectSpace() << std::endl;
std::cout << "Radius: " << (⋆it).GetRadiusInObjectSpace() << std::endl;
std::cout << "Tangent: " << (⋆it).GetTangentInObjectSpace() << std::endl;
std::cout << "First Normal: " << (⋆it).GetNormal1InObjectSpace()
<< std::endl;
std::cout << "Second Normal: " << (⋆it).GetNormal2InObjectSpace()
<< std::endl;
std::cout << "Color = " << (⋆it).GetColor() << std::endl;
it++;
i++;
}
The source code for this section can be found in the file
DTITubeSpatialObject.cxx.
itk::DTITubeSpatialObject derives from itk::TubeSpatialObject. It represents a fiber tracts from Diffusion Tensor Imaging. A DTITubeSpatialObject is described as a list of centerline points which have a position, a radius, normals, the fractional anisotropy (FA) value, the ADC value, the geodesic anisotropy (GA) value, the eigenvalues and vectors as well as the full tensor matrix.
Let’s start by including the appropriate header file.
DTITubeSpatialObject is templated over the dimension of the space. A DTITubeSpatialObject contains a list of DTITubeSpatialObjectPoints.
First we define some type definitions and we create the tube.
We create a point list and we set:
DTITubeType::DTITubePointListType list;
for (i=0; i<5; ++i)
{
DTITubePointType p;
PointType pnt;
pnt[0] = i;
pnt[1] = i+1;
pnt[2] = i+2;
p.SetPositionInObjectSpace(pnt);
p.SetRadiusInObjectSpace(1);
p.AddField(DTITubePointType::FA,i);
p.AddField(DTITubePointType::ADC,2⋆i);
p.AddField(DTITubePointType::GA,3⋆i);
p.AddField("Lambda1",4⋆i);
p.AddField("Lambda2",5⋆i);
p.AddField("Lambda3",6⋆i);
auto ⋆ v = new float[6];
for(unsigned int k=0;k<6;k++)
{
v[k] = k;
}
p.SetTensorMatrix(v);
delete[] v;
p.SetColor(1,0,0,1);
list.push_back(p);
}
Next, we create the tube and set its name using SetName(). We also set its identification number with SetId() and, at the end, we add the list of points previously created.
The GetPoints() method return a reference to the internal list of points of the object.
Then we can access the points using STL iterators. GetPosition() and GetColor() functions return respectively the position and the color of the point.
DTITubeType::DTITubePointListType::const_iterator it
= dtiTube->GetPoints().begin();
i=0;
while(it != dtiTube->GetPoints().end())
{
std::cout << std::endl;
std::cout << "Point #" << i << std::endl;
std::cout << "Position: " << (⋆it).GetPositionInObjectSpace() << std::endl;
std::cout << "Radius: " << (⋆it).GetRadiusInObjectSpace() << std::endl;
std::cout << "FA: " << (⋆it).GetField(DTITubePointType::FA) << std::endl;
std::cout << "ADC: " << (⋆it).GetField(DTITubePointType::ADC) << std::endl;
std::cout << "GA: " << (⋆it).GetField(DTITubePointType::GA) << std::endl;
std::cout << "Lambda1: " << (⋆it).GetField("Lambda1") << std::endl;
std::cout << "Lambda2: " << (⋆it).GetField("Lambda2") << std::endl;
std::cout << "Lambda3: " << (⋆it).GetField("Lambda3") << std::endl;
std::cout << "TensorMatrix: " << (⋆it).GetTensorMatrix()[0] << " : ";
std::cout << (⋆it).GetTensorMatrix()[1] << " : ";
std::cout << (⋆it).GetTensorMatrix()[2] << " : ";
std::cout << (⋆it).GetTensorMatrix()[3] << " : ";
std::cout << (⋆it).GetTensorMatrix()[4] << " : ";
std::cout << (⋆it).GetTensorMatrix()[5] << std::endl;
std::cout << "Color = " << (⋆it).GetColor() << std::endl;
++it;
++i;
}
The source code for this section can be found in the file
ReadWriteSpatialObject.cxx.
Reading and writing SpatialObjects is a fairly simple task. The classes itk::SpatialObjectReader and itk::SpatialObjectWriter are used to read and write these objects, respectively. (Note these classes make use of the MetaIO auxiliary I/O routines and therefore have a .meta file suffix.)
We begin this example by including the appropriate header files.
Next, we create a SpatialObjectWriter that is templated over the dimension of the object(s) we want to write.
For this example, we create an itk::EllipseSpatialObject.
Finally, we set to the writer the object to write using the SetInput() method and we set the name of the file with SetFileName() and call the Update() method to actually write the information.
Now we are ready to open the freshly created object. We first create a SpatialObjectReader which is also templated over the dimension of the object in the file. This means that the file should contain only objects with the same dimension.
Next we set the name of the file to read using SetFileName() and we call the Update() method to read the file.
To get the objects in the file you can call the GetGroup() method. Calls to GetGroup() returns an pointer to a itk::GroupSpatialObject.
The source code for this section can be found in the file
SpatialObjectToImageStatisticsCalculator.cxx.
This example describes how to use the itk::SpatialObjectToImageStatisticsCalculator to compute statistics of an itk::Image only in a region defined inside a given itk::SpatialObject.
We first create a test image using the itk::RandomImageSource
using ImageType = itk::Image< unsigned char, 2 >;
using RandomImageSourceType = itk::RandomImageSource< ImageType >;
RandomImageSourceType::Pointer randomImageSource
= RandomImageSourceType::New();
ImageType::SizeValueType size[2];
size[0] = 10;
size[1] = 10;
randomImageSource->SetSize(size);
randomImageSource->Update();
ImageType::Pointer image = randomImageSource->GetOutput();
Next we create an itk::EllipseSpatialObject with a radius of 2. We also move the ellipse to the center of the image.
Then we can create the itk::SpatialObjectToImageStatisticsCalculator.
We pass a pointer to the image to the calculator.
We also pass the SpatialObject. The statistics will be computed inside the SpatialObject (Internally the calculator is using the IsInside() function).
At the end we trigger the computation via the Update() function and we can retrieve the mean and the covariance matrix using GetMean() and GetCovarianceMatrix() respectively.